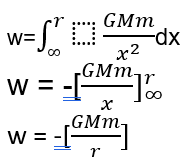Assuming that we are talking about a gravitationally bound system between our current location with respect to the Sun and a distant star. A quick google search reveals that the furthest night star we can see with the naked eye is a little over 4000 light-years away in the constellation Cassiopeia, and has a weight of about 500 solar masses.
The maximum distance we can see is more or less 30 billion light-years. The energy needed to yeet this star to the maximum distance visible to us can see so can be found quite easily through the formula of gravitational potential energy.
The negative sign here indicates that the potential energy is binding in nature. Applying this with respect to the system of our solar system and the star in question. We can find the potential difference between the point where the star stops being visible to us to its current position relative to the Earth. That difference is equal to the total work needed to be done to drag that star from its current location to the nearest point where Gabriel threw it, or in other words the energy needed to do this feat.
The mass of the star= 9.9455 x 10^33 kilograms
The mass of Solar system= 1.9891 × 10^30 kilograms
The distances, r1 and r2 respectively= 3.784
× 10^18 meteres and 2.838 x 10^27 meteres
Constant G=6.67 x 10^-11
Thus the energy needed to move the single further star we can see outside our visual range, now this is as accurate as I can get which is by 15 decimal points- 1.76268475440451 x 10^39 Joules
That is merely the energy needed to move the star which according to google is the furthest one we can see in the night sky and gravity is a force that is inversely proportional to the square of the distance. Meaning, as we get further the force needed decreases
exponentially. So, the stars which are closer to us would require literally trillions to septillions times more energy needed to perform the same feat. Also, the gravity of the sun is obviously not the only force that's keeping these stars in their place. There are planets, stars, and galaxies whose gravity also binds these stars. Then there's the fact that these stars have varying masses. Then there's the fact that Fiamma can manipulate every star in the universe, not just the measly amount we see.
There are 400 billion stars in our night sky
Assuming the same conditions, to yeet them all outside our visible range we need- 7.05073901762 x 10^52 joules of energy.
That's about galaxy level and this is an exponential lowball, the actual energy should be order of magnitudes higher considering the inverse square law and the distances involved..
, like the characters are the most generic shit ever and the MC is Kirito number 2234322545 , Touma and friends are way more enjoyable.